斷裂韌性是評估材料抗裂紋擴展能力的關鍵參數。在設計和制造過程中,了解材料的斷裂韌性可以幫助選擇合適的材料,確保設備在使用過程中的安全性。對于已經投入使用的設備,評估材料的斷裂韌性可以預測設備在運行過程中可能出現的裂紋擴展情況,從而預防事故的發生。傳統的斷裂韌性測試方法(如單邊缺口梁測試和緊湊拉伸測試)需要較大的樣本和復雜的加載程序,不適用于正在服役的材料和小樣本情況。因此,鄭州大學的張建偉教授團隊提出了一種基于劃痕測試的替代方法,用以測定金屬材料的斷裂韌性。
通過拉伸測試和緊湊拉伸測試得到四種不同金屬材料的拉伸和斷裂性能,測試所用試樣如圖1所示。通過維氏壓頭對材料進行劃痕測試,圖2為劃痕測試示意圖。將通過劃痕測試得到的斷裂韌性與緊湊拉伸測試得到的斷裂韌性進行對比,以驗證替代方法的準確性。

圖1 (a)拉伸測試與(b)緊湊拉伸測試試樣示意圖。

圖2 劃痕測試示意圖(a)正視圖,(b)側視圖,(c)俯視圖。
基于線性彈性斷裂力學的假設可以得到刮頭切向力與材料斷裂韌性Kc、壓頭與樣品表面的夾角θ、壓頭與材料接觸面的周長p等有關(式1)。通過對該式進行簡化可得本文考慮拉伸強度和延展性后(UT為拉伸強度和斷裂伸長率的乘積)所修正的線性彈性斷裂力學模型(Modified Model)(式2)。通過如圖3所示的流程圖可以經由兩次不同深度的劃痕測試來測得材料的斷裂韌性。
(1)
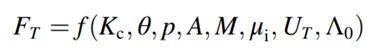
(2)
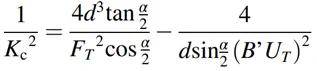

圖3 通過修正的線性彈性斷裂力學模型得到斷裂韌性的流程圖。
通過現有的線彈性斷裂力學(LEFM)模型、Akono的微觀能量尺寸效應定律(MESEL)模型、Hubler的MESEL模型、Liu的MESEL模型以及文章所使用的修正的線性彈性斷裂力學模型將測試得到的參數進行計算,得到不同的斷裂韌性結果,不同模型之間的差異如圖4所示。

圖4 用來得到斷裂韌性的不同理論模型。
將結果與緊湊拉伸測試所得到的斷裂韌性進行了比較。實驗結果表明,修正模型在計算金屬材料的斷裂韌性方面具有較高的準確性(圖5)。但劃痕深度較小時,劃痕的產生主要由塑性變形導致,劃痕中并沒有明顯的裂紋,此時該模型對斷裂韌性的計算準確度不夠理想(圖6)。

圖5 不同材料LEFM模型、Akono的MESEL模型、Hubler的MESEL模型、Liu的MESEL模型以及修正的線性彈性斷裂力學模型所得到的斷裂韌性與緊湊拉伸測試(CT)得到的斷裂韌性進行對比,(a)18CrNiMo7-6,(b)DP800,(c)4140,(d)4340。

圖6 不同法向載荷下18CrNiMo7-6的劃痕微觀形貌,(a)5N;(b)10N;(c)15N;(d)20N;(e)25N;(f)30N;(g)35N;(h)40N;(i)45N;(j)50N。
研究提出了一種基于劃痕測試的金屬材料斷裂韌性測試方法,能夠較為準確地評估材料的斷裂韌性。該方法僅需進行兩次不同劃痕深度的測試,即可估算未知材料的斷裂韌性。在理論模型的開發中,結合材料的微觀和宏觀特性可以進一步提高模型的準確性和適用性。但該方法是否能推廣到脆性高分子材料中還需繼續進行驗證。
相關研究論文“Fracture toughness testing of metallic materials based on scratch tests"已發表在《Theoretical and Applied Fracture Mechanics》
版權所有 © 2025 凱爾測控試驗系統(天津)有限公司 備案號:津ICP備18003419號-2 技術支持:化工儀器網 管理登陸 GoogleSitemap